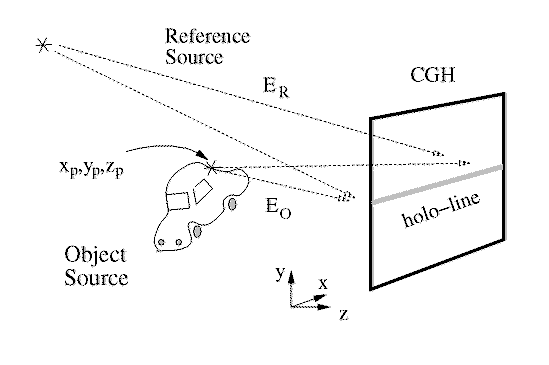
General geometry for HPO CGH.
This paper is a revision of paper 1667-04 presented at the SPIE/IS&T conference Electronic Imaging '92, February 1992, San Jose, California. The paper presented there appears (unrefereed) in SPIE/IS&T Proceedings Vol. 1667.
NB: This is an HTML version of this paper. Equations and algebraic variables are not quite finished, so some imagination is required by the reader. A PostScript version of this paper and a (Unix) compressed Postscript version are also available.
A holographic fringe pattern is computed by numerically simulating the physical phenomena of light diffraction and interference[4]. Computation of holographic interference patterns often utilizes the fast Fourier transform (FFT) algorithm. Though relatively fast for images composed of discrete depth surfaces[5],[6], this approach becomes slow when applied to images that extend throughout an image volume. A more general ray-tracing approach computes the contribution at the hologram plane from each object point source. This method can produce arbitrary 3-D images, including image-plane holograms (i.e., images that lie in the vicinity of the hologram), a case that is more suitable for various display geometries. However, this method is slow, since it requires one calculation per image point per hologram sample. As presented in this paper, the application of several methods of reducing computation complexity leads to computation times as short as 1 s on a data-parallel-processing supercomputer. First, a bipolar intensity representation of the holographic interference pattern is applied and shown to eliminate unwanted image artifacts and simplify calculations without loss of image quality or generality. Second, a look-up table approach is described and shown to provide a further speed increase and to reduce computation to a minimum. Finally, exemplary computation times are presented.

General geometry for HPO CGH.
The information content of a CGH must be reduced to a size and format that can be manipulated by existing computers. Eliminating vertical parallax reduces CGH information content by at least a factor of 100 by reducing the vertical spatial frequency content from roughly 1000 to roughly 10 lp/mm. Sacrificing the size of the viewing zone (i.e., reducing the required horizontal pitch) and the size of the hologram also reduces the amount of data in the CGH. In the first generation MIT system, the data content (space-bandwidth product) of the CGH was as low as 2 Mbytes[2].
In optical holography[8], the object light and the reference light are incident at the plane of the hologram, represented with spatially varying complex time-harmonic electric field vectors, Eo and Er. It is assumed that both are mutually coherent sources of monochromatic light. For this analysis, the units of an electric field amplitude are normalized so that the square of magnitude corresponds to optical intensity; the polarizations are assumed to be identical and for simplicity are not specified. The total time-harmonic electric field incident on the hologram is the interference of the light from the entire object and the reference light, Eo + Er. The total intensity pattern,
I_total =|Eo|^2+|Er|^2+2 Re{Eo Er*} (1)
is a real physical light distribution comprised of three
components.
The first term is the object self-interference, a spatially varying
pattern that is generated when interference occurs between light
scattered from two different object points. During image
reconstruction, this component of the holographic pattern is
unnecessary and often produces unwanted image artifacts. In optical
holography, a common solution is to spatially separate the
object self-interference artifacts from the reconstructed image by increasing the
reference beam angle to at least three times the angle subtended by
the object. However, in computational holography, a large reference
beam angle is a luxury that one does not have. Instead, the solution
is simply to exclude the object
self-interference during
computation.
The second term in Itotal is the reference beam intensity and
represents a spatially nearly invariant (dc) bias that increases
the value of the intensity throughout the hologram. In computational
holography, the reference bias can be left out, since the CGH will eventually
be normalized.
(Normalization is the numerical process that
limits the range of the total fringe pattern by introducing an offset and a
scaling factor to tailor the fringe pattern to fit
the requirements of a display system.)
Finally, the third term
is the interference
between the object wave front and the reference beam. This fringe
pattern -- called Ib -- contains
the
holographic information that is necessary and sufficient to image
reconstruction.
Phi_p(x) = k r_p(x) + phi_p (2)
where
r_p(x) = [(x-x_p)^2 + z_p^2 ]^{1/2}
is the oblique distance to a location on the holo-line and is
a function of x.
The wave number is k=2pi/lambda, where
lambda is the free-space wavelength of the light. The
time-harmonic representation of the total object field for a single
holo-line is
Ny
---
\
Eo(x) = / e(x) a_p/r_p(x) exp{ i Phi_p(x) } (3)
---
p=1
where N_y
is the number of object points contributing to this
particular y-valued holo-line.
Finally, to avoid singularities, it is assumed that the
magnitude of z_p is never less than some small amount, e.g.,
10 lambda.
In Eq. 3, the expression e(x) is an envelope function used to specify the region of contribution for a given object source. In its simplest form, e(x) is equal to unity within the region of contribution of point p, and equal to zero for all other values of x. The envelope function e(x) provides a means with which to limit the spatial frequencies of the holographic fringe pattern to avoid aliasing in the CGH at the extreme angles of object light incidence. Object ``light'' used to compute the CGH must have a minimum angle of incidence that is greater than that of the reference beam to produce non-overlapping real and virtual reconstructed images. At the other extreme, the total angle subtended by the incident reference and object beams cannot be so large as to give rise to spatial frequencies that cannot be adequately represented given the sampling pitch. For a horizontal sampling pitch of 1/d, the maximum spatial frequency (f_max) that can be represented is 1/2d, according to the Nyquist Sampling Theorem. Higher spatial frequencies cause aliasing and destroy image quality. In addition to providing anti-aliasing, e(x) is used for the purposes of image occlusion[9] and advanced image lighting models, resulting in a more realistic looking image.
The reference beam Er is a point source at some specific location (xr, zr) with a horizontal angle of incidence theta_r = arctan(xr/zr) and curvature in the x dimension only; it is collimated in the y dimension. The time-harmonic representation of the reference beam field at any holo-line is
Er(x) = ar/rr exp{ i Phi_R(x) } (4)
where
Phi_R(x)=k[(x-xr)^2+zr^2]^{1/2}
and ar/rr is the magnitude (approximated as constant
versus x) of the
reference wave at the center (x=0) of the hologram.
Ib(x) =
Ny
---
\
2 Re{ [ / e(x) a_p/r_p(x) exp{ iPhi_p(x) } ] [ ar/rr exp{iPhi_R(x)} ]* ,
---
p=1
Ny
---
\
= 2 ar/rr { / Re{ e(x) a_p/r_p(x) exp{iPhi_p(x)-iPhi_R(x)} }
---
p=1
and finally simplified to:
Ny --- \ Ib(x) = 2 ar/rr / e(x) a_p/r_p(x) cos[Phi_p(x)-Phi_R(x)] --- p=1The right-hand side of Eq. 5 is simply a scaled sum of the real-valued cosinusoidal fringe pattern resulting from the interference of point source p with the reference beam. The bipolar intensity approach is to compute only Ib (instead of Itotal), using only these real-valued cosinusoidal fringes.
The computational advantage of the bipolar intensity approach is readily seen by comparison to computation of the full interference pattern, Itotal. The latter method requires the use of complex-valued arithmetic, i.e., manipulating both the real and imaginary parts of the object and reference light. In comparison, the bipolar intensity approach uses only real-valued cosinusoidal fringes; to generate the CGH, these real values are simply summed. A speed-up factor of 2 is expected.
After an intensity pattern has been computed, it must be normalized to satisfy the output device requirements of the CGH display system. Because normalization generally scales the entire pattern, the leading factor of 2 ar/rr on the right side of Eq. 5 is hereafter excluded. The reference beam intensity (the square of ar/rr) is no longer meaningful. This makes physical sense when considering that in optical holography, the purpose of choosing an optimal reference beam intensity ratio (relative to the object light) is to provide a sufficient offset and scaling of the interference fringes to keep them within the range of sensitivity of the recording medium. Computationally, offset and scaling are provided automatically during normalization. Therefore, the factor of 2 ar/rr is set arbitrarily to unity. Substituting the definition of Phi_p(x) (Eq. 2), Eq. 5 becomes
Ny
---
\
Ib(x) = / e(x) a_p/r_p(x) cos[k r_p(x) + phi_p - Phi_R(x) ]
---
p=1
which is hereafter called the bipolar fringe method of CGH
computation. No reference beam ratio needs to be specified during
computation, and bias buildup is not an issue. Compare this bipolar
intensity method to the physical process occurring in some
photorefractive crystals[10] (e.g., lithium niobate), in
which uniform (dc) intensity is not recorded due to the material's
negligible response to intensity patterns with low spatial
frequencies. Researchers exploit this absence of bias build-up in
order to sequentially expose multiple holographic intensity patterns.
Equation 6 must be altered so that Ib(x) is expressed in terms of discretized image point locations instead of x_p and z_p. The expressions [x_p] and [z_p] are used to represent x_p and z_p rounded-off to the nearest values of X_i and Z_i. Therefore, the only change made to Eq. 6 is to substitute [x_p] and [z_p] for x_p and z_p in the expression for r_p(x) (in Eq. 2). (Note that the variable x is already discretized due to the the sampled nature of the CGH. The horizontal pitch is dictated by the intended display device.) An efficient look-up table should include all of the spatial dependence included in the right-hand side of Eq. 6. Therefore, the elemental fringe look-up table T(Xi,Zi,x) is defined as:
def
T(Xi,Zi,x) === e(x)/r_i(x) cos[ k r_i(x) - Phi_R(x) ]
where
r_i(x) = [(x-X_i)^2 + {Z_i}^2 ]^{1/2}.
The table looks like an array of cosinusoid-like fringes that
have an approximately linear chirp in spatial frequency with respect
to x. The rate of chirp is a function of the point source depth
Z_i, and the horizontal position of the fringe is a function of
X_i.
To incorporate anti-aliasing, e(x) is set to unity within the region
of contribution, and zero elsewhere.
(This binary representation of e(x) is for
simplicity.
Any further
variation in e(x) can be dealt with during computation, or
with additional look-up tables.)
When utilizing the look-up table approach, phi_p is set to zero
(or randomized) for
simplicity.
Once precomputed, the table T is used during the computation of a CGH to represent a specific image. Rather than having to compute a cosinusoidal fringe each time one is needed (as indicated in Eq. 6), the lookup table maps each ([x_p],[z_p]) to the appropriate elemental fringe pattern. Thus, Ib(x), expressed in terms of the precomputed table, is
Ny
---
\
Ib(x) = / a_p T([x_p],[z_p],x)
---
p=1
Since each holo-line is computed using the same
ER(x), one precomputed table is used in the computation
of every holo-line.
Computation for a given holo-line at vertical position y is as
follows:
- For every point on scan plane y: - Round off x_p and z_p to [x_p] and [z_p] to index the desired elemental fringe. - For each x sample in Ib(x): Scale T([x_p],[z_p],x) by a_p. Accumulate a_p T([x_p],[z_p],x) in Ib(x).After each holo-line is computed (at each value of y), then normalization and output are performed depending on the specific display system.
The issue of object point phase phi_p must be examined to justify setting the phase to zero for all points. Phase is invisible to the viewer. Object phase is important only in the interactions among image points. If the discretization steps of X_i and Z_i (typically 150 microns and 1000 microns) are much larger than the spot size of the display system, no overlap occurs between image points. In this case, as was the case in the MIT holographic display, restricting phi_p does not limit the size, depth, or quality of an image. Therefore, the relative phases phi_p are unimportant and can be arbitrarily set to zero. (If nonzero phase values are required, two look-up tables in quadrature are sufficient for this more general case.) In some applications, phi_p can be randomized to make more efficient use of the dynamic range. A random phase factor for each point can easily be incorporated into the look-up table.
Look-up table quantization increases image noise due to the loss of accuracy. In practice, however, table quantization has little effect on the final image quality since Ib(x) must be quantized when stored in the output framebuffer of the computing system. For example, in the first generation MIT system, the framebuffer used was capable of storing 6M samples, each represented by 8 bits, giving the output data 256 possible quantized levels. Typically, the object light from at least 64 objects points overlap at a single sample of Ib(x). If each object point has an average amplitude of 1.0, then a typical elemental fringe pattern from the look-up table will occupy only about 256/64 = 4 different levels in the framebuffer. Therefore, a four-level look-up table is well suited to this display system.
During the table look-up computation, x_p and z_p are rounded off to [x_p] and [z_p], the nearest values of X_i and Z_i, making Dx = x-[x_p] for a given image point p. In terms of these variables, the expression for r_p (see Eq. 2) becomes a function of [z_p] and Dx. Looking at Eq. 6, the envelope function e(x) is actually a function of Dx/z_p, since e limits the angular direction of light propagation (equal to arctan [Dx/z_p]). Thus, Eq. 6 becomes
Ny
---
\
Ib(x) = / e(Dx) a_p/r_p([z_p],Dx) cos[k r_p([z_p],Dx)-Phi_R(x)]
---
p=1
where
r_p([z_p],Dx) = ({Dx}^2 + {[z_p]}^2 )^{1/2}.
Now
only Phi_R(x)
is an explicit function of x (rather than of Dx),
and must therefore be manipulated
to become a function of Dx.
First, by restricting the reference beam
to be a plane-wave (i.e., rr goes to infinity), the reference phase is simply
Phi_R(x) = kr*x,
where kr = k sin(theta_r).
The second restriction is that X_i be
discretized by
2 pi / kr,
making every possible value of
kr Dx
differ by exactly 2 pi m for a given value of x,
where m is some unimportant integer value.
Consider that when computing the cosine of total phase, any
integer multiple of 2 pi is ignored.
Therefore, Phi_R(x) can be expressed as
Phi_R(x) = kr x + 2 pi m = kr Dx
for all values of X_i.
Finally, Eq. 6
can be expressed as a function of only two variables
[z_p] and Dx:
Ny --- \ Ib(x) = / e(Dx) a_p/r_p([z_p],Dx) --- cos[k r_p([z_p],Dx) - krDx ] . p=1A corresponding look-up table of rank two can be used, with the indices [z_p] and Dx.
Essentially, given the restriction of a plane-wave reference beam, the elemental fringe patterns are shift-invariant in x for any [x_p] equal to an integer multiple of 2 pi / kr. The first advantage is a reduction in size equal to at least the number of discrete values of [x_p] used in the rank-three table (~100 or more). The second advantage is that X_i is discretized in very small steps (2 pi/kr ~10 microns) without increasing the size of the rank-two table; the horizontal image discretization is much finer than can be seen by the human visual system. The only drawback to the rank-two table approach is the requirement that the reference beam be a plane wave. However, this is a common case, and is applicable to many display architectures. As demonstrated in Section 6, this contraction of rank is especially useful when implemented on a standard serial-processing computer.
To facilitate rapid computation of stereogram-type CGHs, the precomputed table is indexed by image x-position and view-angle (rather than by X_i and Z_i). Furthermore, the table can be reduced to rank two as described above, making the table much smaller. Stereogram CGHs have been computed and displayed on the MIT real-time holographic display system. A major advantage to the stereogram approach is the integration of sophisticated lighting and shading models in the computer graphics rendering process to produce extremely realistic images possessing important 3-D image characteristics, such as occlusion (overlap) and specular reflections.
Table 1 contains the computation times (time per image point) using different approaches. ``Itotal (complex)'' The common traditional case was ``Itotal (complex)'' where Eqs. 1, 2, 3 and 4 are combined to compute Itotal . The ``Bipolar intensity'' approach was simply the computation of Ib instead of Itotal . The ``Look-up table'' method employed the precomputed elemental fringe table, represented in the memory of the CM2 as 2 bits per sample. As each object point was read from an input file, the position (x_p,z_p) was used to index the table in each processor. At each x, conditional logic was performed on each of the 2 bits, and the appropriate fractions of the object point amplitude were accumulated into the register representing Ib. Since this was performed in parallel for all 32K samples of Ib(x), rapid computation of images was possible. The time per point listed in Table 1 is the amount of computation time required (on average) to accumulate the fringe pattern contribution of a single object point source. These numbers were obtained by computing holograms of several different test images of varying complexity. For comparison, the different computational approaches were also implemented on a serial computer, a Sun 4 workstation, and the results are included in Table 1.
Computation method CM2 Sun4 ------------------ --- ---- I_total (complex) 2.180 ms 943.4 ms Bipolar intensity 1.135 ms 486.2 ms Look-up table 0.084 ms 22.1 msIn all cases, the computation time per point was simply the total execution time divided by the number of points processed. Computation time scaled linearly with image complexity; despite the different image complexities (from 100 to 50,000 points), the time per point quotient remained within a 2% range. Table 1 shows that, as expected, the bipolar approach was roughly twice as fast as the traditional complex method of computation. This was evident on both the parallel-data and serial machines. By using the look-up table, the CM2 speed increased by a factor of 26; the serial machine was faster by a larger factor of about 43. (The CM2 actually has an array of floating-point math accelerator chips that are no longer utilized in look-up table calculations.) The simpler serial machine gained more from the use of a look-up table.
For practical purposes, additional procedures that are independent of object complexity must be performed, including normalizing the computed holographic pattern and moving it into the frame-buffer. Therefore, a generally fixed overhead time must be added when expressing the total time to compute and output the holographic pattern. For a 6 megabyte holographic pattern, this time is approximately 400 milliseconds (or less) on the CM2. For example, the actual time to compute and display a 10,000-point image using the look-up table approach is 10000 x 0.084 ms+400 ms = 1.24 s, or less.
In the current MIT display system, simple images generated from 3-D computer graphics databases contain only a few thousand points. Using the fastest look-up table computation method, images are computed at a rate of over 1 frame per second. (In many cases, computation time was actually less than the overhead time spent loading the computed CGH into the framebuffer!) To demonstrate interactivity, the viewer can turn any of several dials (interfaced to the computer) in order to translate the image in horizontal, vertical, and depth locations, to change its size, and to spin it along different axes of rotation. In addition, a simple drawing program was written in which the user can move a 3-D cursor to draw a 3-D image that can also be manipulated.
It must also be noted that the holographic patterns computed by these three approaches were equivalent, with the following exceptions. Use of the bipolar intensity eliminated object self-interference and dc terms, making the CGH brighter and less noisy than when using the complex Itotal method. The look-up table approach resulted in a pattern that was identical to the bipolar intensity approach, with the addition of some quantization noise if a 2-bit table was used. However, for objects of sufficient complexity, this quantization noise was comparable to that of the more straightforward approaches, due to the quantized nature of the output frame-buffer device used in the system.
The overall speedup demonstrated here is remarkable. CGH computation that traditionally would require several minutes or hours on a mainframe computer is reduced to 1 s. The look-up table approach, by eliminating the need for all mathematical functions other than simple addition and multiplication, is especially advantageous when only minimal computing power is available for CGH computation. Essentially, the table stores a large array of holographic basis functions, the weighted sum of which is sufficient to describe the CGH corresponding to any arbitrary image. Given adequate memory space to hold the precomputed elemental fringes, it is possible to design a dedicated CGH computer that requires no floating-point mathematics and uses only integer addition (and perhaps bit shifting for normalization purposes). Such a simple machine can be implemented in parallel, e.g., one computer per holo-line, to achieve real-time CGH computation without the need for an expensive supercomputer. It is interesting to note that the 2-bit table approach implemented on the CM2 computes a CGH using only two conditional additions per image point per sample, emphasizing the computational simplicity made possible by the use of a look-up table.
The look-up table is the simplest possible algorithm for computing CGH from the discrete-point object model. To achieve faster speeds, future work involves an approach in which a higher level of object description is processed during CGH computation. Also, to increase speeds on workstation computers, it may be useful to utilize certain specialized hardware such as computer graphics rendering engines or digital signal processing boards used for image coding and decoding.
Analytical simplification of the physical model of light interference made possible this increase in speed. These concepts can be applied to other types of holograms. The bipolar intensity method is applicable to all types, including full-parallax CGHs. The use of the bipolar intensity summation method, whether directly or through a look-up table, eliminates object self-interference noise, eliminates the need to adjust a reference beam ratio, and produces an optimally bright image by eliminating unnecessary dc intensity bias. The look-up table approach can be applied to full-parallax holograms, although by requiring both x and y indices, the precomputed table (data arrays of rank five, reduced to rank three using the method shown) would require enormous amounts of memory space. In the future, as computational power increases, the simplification of computation presented here will continue to provide speed-up for any CGH application.
This research on computational electronic holography has been supported in part by the Defense Advanced Research Projects Agency (DARPA) through the Rome Air Development Center (RADC) of the Air Force System Command and the Naval Ordnance Station, Indian Head, Maryland, contract #N00174-91-C-0117, and by the TV of Tomorrow consortium at the MIT Media Laboratory.
1
P. St. Hilaire, S. A. Benton, M. Lucente, M. L. Jepsen, J. Kollin, H.
Yoshikawa and J. Underkoffler.
``Electronic display system for computational holography''.
In Practical Holography IV, Proceedings of the SPIE,
volume 1212-20, pages 174-182, Bellingham, WA, 1990.
2
S. A. Benton.
``Experiments in holographic video imaging''.
In P. Greguss, editor, Holography, Proceedings of the
SPIE, volume IS#08, pages 247-267, Bellingham, WA, 1991.
3
P. St. Hilaire, S. A. Benton, M. Lucente, J. Underkoffler and H. Yoshikawa.
``Real-time holographic display: Improvements using a multichannel
acousto-optic modulator and holographic optical elements''.
In Practical Holography V, Proceedings of the SPIE,
volume 1461-37, pages 254-261, Bellingham, WA, 1991.
4
W. J. Dallas.
Topics in applied physics.
In B. R. Frieden, editor, The Computer in Optical Research,
volume Vol. 41, chapter 6: "Computer-Generated Holograms", pages 291-366.
Springer-Verlag, New York, 1980.
5
D. Leseberg and C. Frere.
``Computer-generated holograms of 3-D objects composed of tilted
planar segments''.
Applied Optics, 27(14):3020-3024, July 1988.
6
D. Leseberg.
``Computer-generated holograms: display using one-dimensional
transforms''.
Journal of the Optical Society of America, 3(5):726-730,
May 1986.
7
D. Leseberg and O. Bryngdahl.
``Computer-generated rainbow holograms''.
Applied Optics, 23(14):2441-2447, July 1984.
8
P. Hariharan.
Optical Holography: Principle, Techniques and Applications.
Cambridge University Press, Cambridge, 1984.
9
J. S. Underkoffler.
``Toward Accurate Computation of Optically Reconstructed
Holograms''.
Master's thesis, Massachusetts Institute of Technology, June 1991.
10
A. M. Glass.
``The photorefractive effect''.
Opt. Eng., 17(5):470-479, 1978.